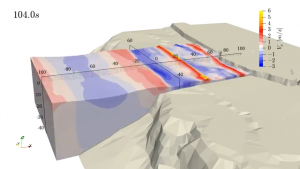
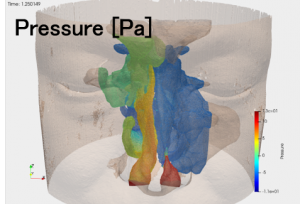
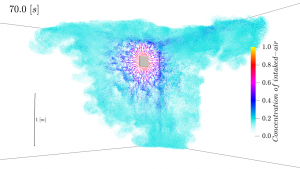
ビル等に導入される空調設備では,矩形断面の管路が広く用いられています.この場合、管路上流の送風機や管路内部で発生した騒音が,管路を伝播して居室まで響き,騒音問題を引き起こすことがあります.今回は,上流の送風機による騒音を対象に,管路内部を音波が伝播する状況を音響解析により予測・可視化します.
解析手法と計算条件
音の距離減衰
面音源から発する管路内(径一定)の平面波では,管路径より波長が長い場合,音響エネルギーの距離減衰がほとんど発生せず、離れた場所に音を伝えるために活用されます(伝声管など).騒音についても同様で,管路幅より長い波長の場合、管路出口まで伝播することが危惧されます.
騒音の周波数特性
空調用送風機から発生する騒音の周波数は,500 [Hz]前後の周波数帯で80 [dB]前後の音圧レベルのピークを有することが知られています.音が共鳴すると,音源よりも大きな音圧レベルになる可能性があるため,計算条件には,音源の周波数に共鳴を考慮する必要があります.
音響解析手法(FDTD法)
管路内部の音圧場の予測にあたり,音響波動方程式に基づいた音響解析手法のうち,3次元空間を対象とした時間領域差分法 : Finite Difference Time Domain (FDTD) 法を採用します.
音響解析手法
□ 時間領域差分法 : Finite Difference Time Domain (FDTD)
□ 有限要素法 : Finite Element Method (FEM)
□ 境界要素法 : Boundary Element Method (BEM)
短径管路とガイドベーン
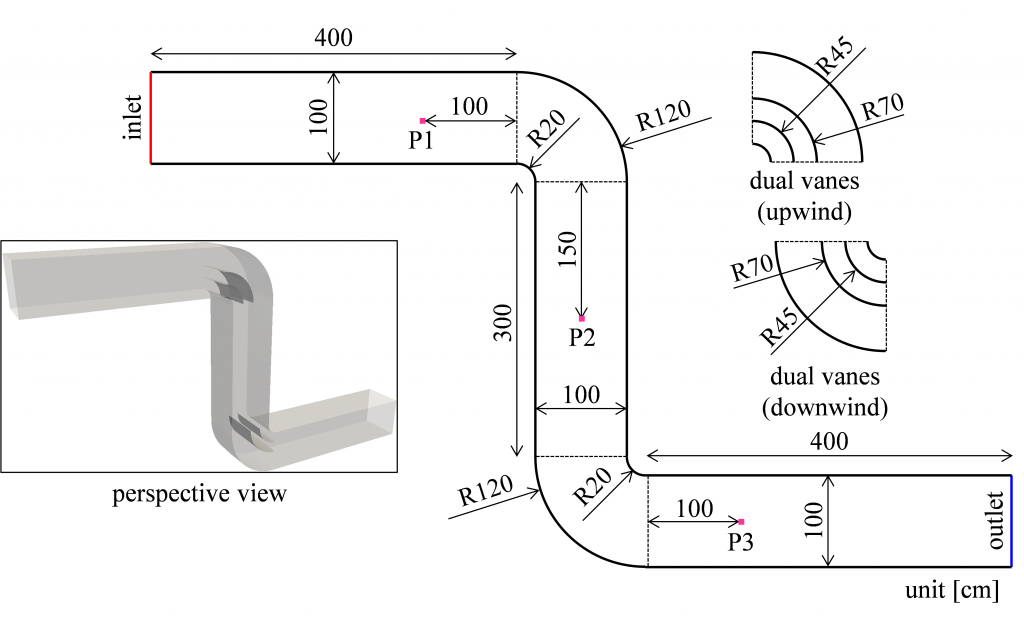
矩形管路とガイドベーンの寸法(中央断面表示),および音圧の時系列データの測定点は,右図のとおりです.なお,矩形管路の断面は1 [m]四方の正方形です.
左下図のように,2枚羽のガイドベーンをエルボー部に導入することで効果的に圧力損失が低減できます.
詳細は、こちらで解説しています▶.
計算格子
計算格子は,一辺Δx = 2[cm]の立方体格子を用います.最も波長が短いCase5a/Case5bの波長は50 [cm]程度なので,単一波長を25格子程度に分割する格子幅です.
計算結果
ガイドベーンなし
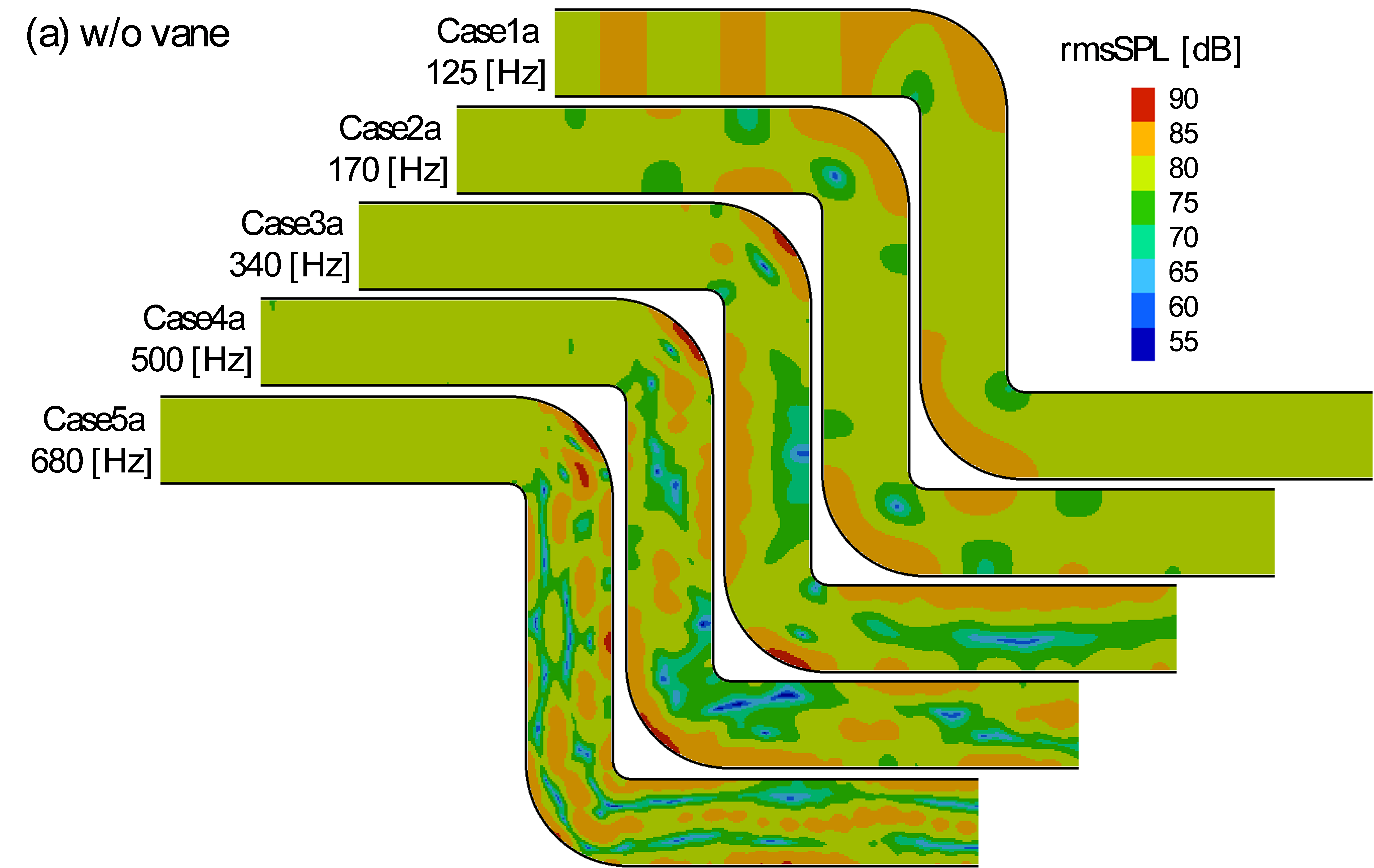
管路径よりも波長が長い125/170 [Hz](Case1a/Case2a)では,管路出口での音圧レベルの減衰はほとんど確認できませんでした.
また,波長が短い340/500/680 [Hz](Case3a/Case4a/Case5a)では,管路出口において音圧の局所分布が見られたものの,音圧レベルの減衰は確認できませんでした.
Case3a~Case5aでの局所分布は,エルボー部での音波の複雑な共鳴により、平面波が崩壊したためと考えられます.また,音圧レベルの減衰が認められなかったことから,音圧の時空間変動に対し,時間刻みと格子幅が妥当だったと言えます. 今回の管路長では,音圧レベルの減衰は認められませんでしたが,理論的には,伝播方向が乱雑になることで,音響エネルギー(音圧)の散逸が想定されます.
ガイドベーンあり
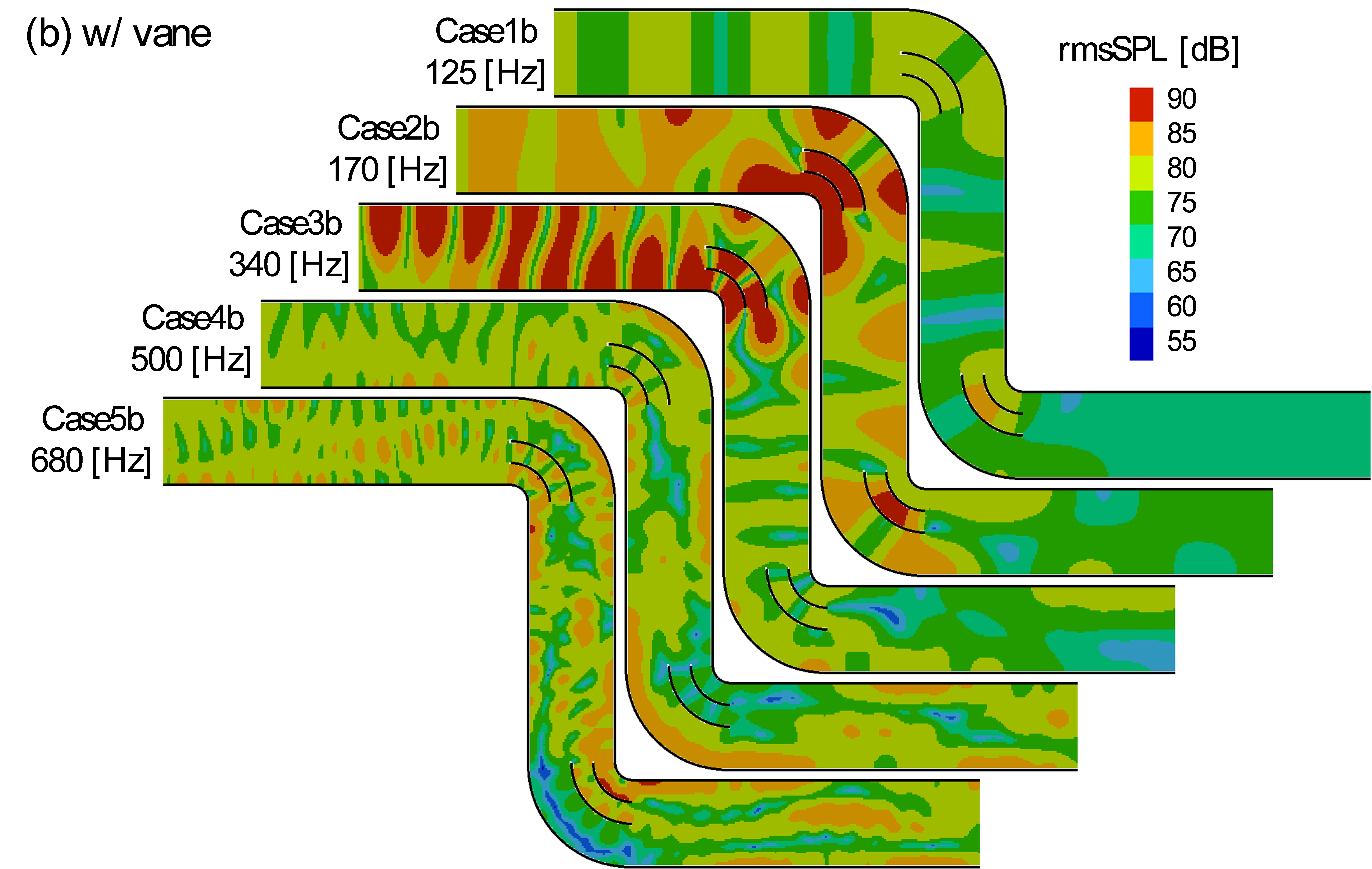
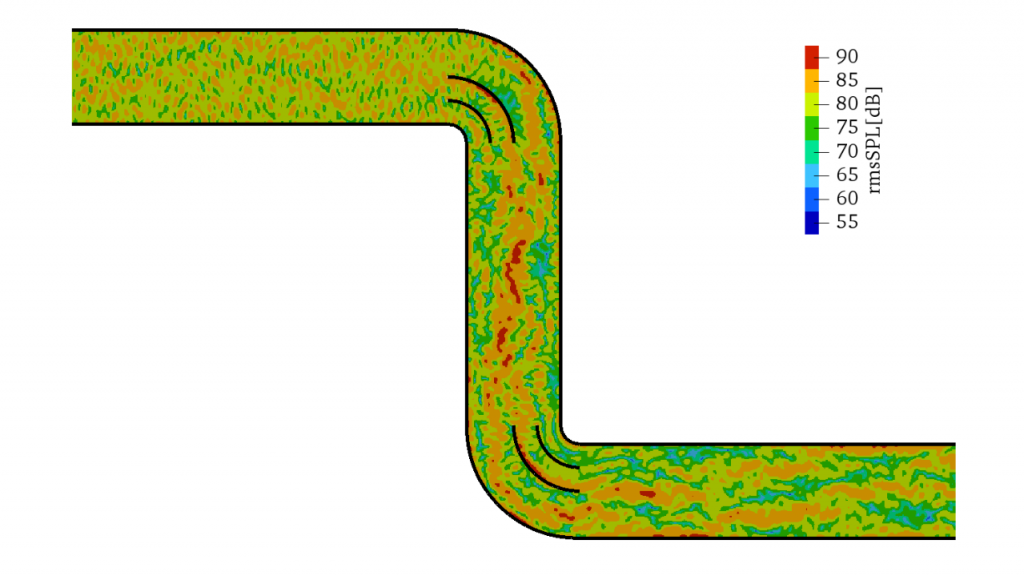
125, 170, 340 [Hz]の音源(Case1b ~Case3b)では,5 [dB]ほどの音圧レベルの減衰が期待できそうです.また500/680 [Hz]の音源(Case4b/Case5b)では,ベーンがない場合と同様,局所的な空間分布が発生するものの,全体的な音圧レベルの減衰はあまり見られませんでした.
これは,低周波音がガイドベーンによって上流側に反射されるためと考えます.一方,高周波音は複雑に共鳴しながら,ガイドベーンの間をすり抜けていき,管路径より長い波長の音波に対しては,ガイドベーンにより音圧レベルの減衰効果が期待されます.
おまけ : 周波数 2 [kHz]での音圧レベルの空間分布(ガイドベーンあり)
右図は,音源の周波数2 [kHz],一辺が1 [cm]の計算格子での音圧レベルの空間分布です(Case6b).管路内では至る所で共鳴が発生している様子が確認できますが,それによる顕著な音圧レベルの減衰は見られません.