風向に対して回転軸が垂直な風車は、垂直軸風車(VAWT: Vertical Axis Wind Turbine)と呼ばれます。垂直軸風車には、風向が頻繁に変化する条件下でも効率良く動作するという利点があります。ここでは代表的な垂直軸風車であるサボニウス風車とダリウス風車の回転メカニズム(風の並進運動が風車の回転運動に変わるメカニズム)を流体力学的な視点を踏まえて概説します。また、最後に減風装置やドローンローターとしての応用を簡単に紹介します。
平板の自励回転
垂直軸風車について考える前に、自励回転する平板について説明します。名刺やカード(平板)を空中で手放すと、一方向に回転しながら落下する様子を観ることができます。この平板の回転運動は自励回転: autorotationと呼ばれます。(手放すときの平板の角度を変えると、自励回転せずにゆらゆらと落ちていく運動: flutteringを観ることができます。)落下している平板から見ると、平板は落下速度相当の風を受けていると考えられます。平板先端の回転の速さUは風の速さVによるので、これらの比である周速比 λ(= U/V)を用いて自励回転の速さを表します。平板の自励回転ではλ< 0.5程度となることが知られています。
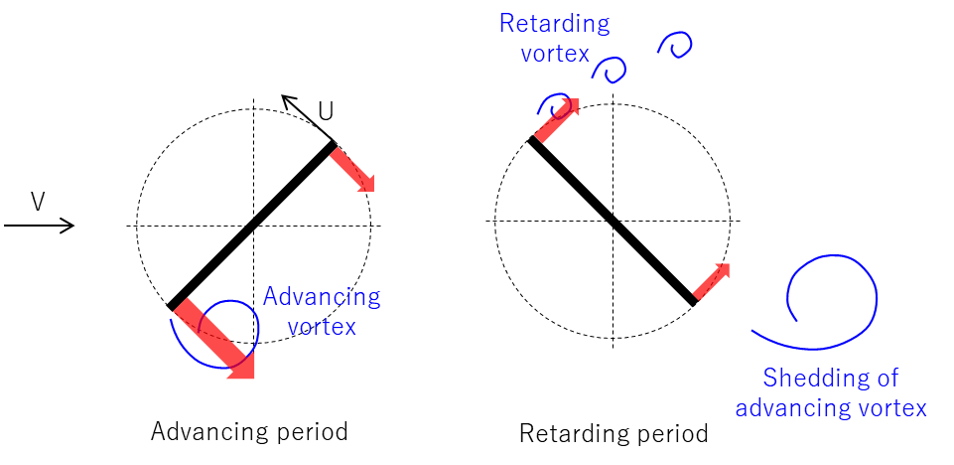
図1のように平板が左図の角度で左から風を受けているとき(advancing period)、平板の下側で強い渦(advancing vortex)が成長します。渦は低圧なので平板は渦に吸い寄せられ、反時計まわりの大きい回転モーメントが生じます。その後、右図の角度まで回転すると、平板から強い渦が離脱して回転モーメントが失われますが、慣性が十分に大きければ回転が弱まりながらも次のadvancing periodまで回転が維持されます。垂直軸風車においてもブレードが推力を生む状態とそうでない状態を交互に繰り返しながら自励回転が維持されます。
サボニウス風車
平板がI字断面のブレードだとすると、サボニウス風車はS字断面のブレードだと考えられます。先ほどと同様に左から風を受けているとき、S字の下側は効率良く風を捉えるのに対して、S字の上側は風を受け流しやすい形状をしています。そのため、S字の下側に大きい回転モーメントが生じ、反時計回りの回転が強められます。ただし、S字の下側は風を捉えて進むので、風より速く進むことはできません。そのため、サボニウス風車の周速比はλ< 1となり、λ≅ 1のとき最も効率良く風を受けて回転します。サボニウス風車は、ブレードが風に押されることで動力を得るため、抗力型風車に分類されます。

ダリウス風車
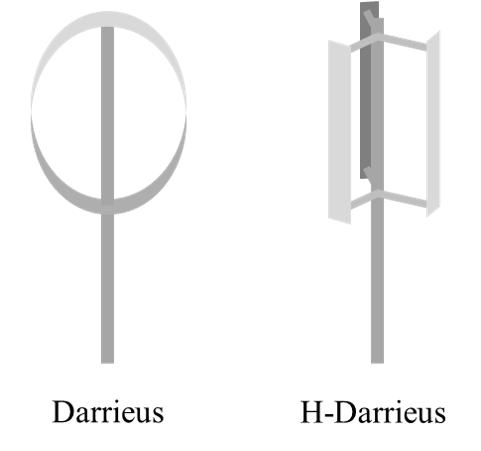
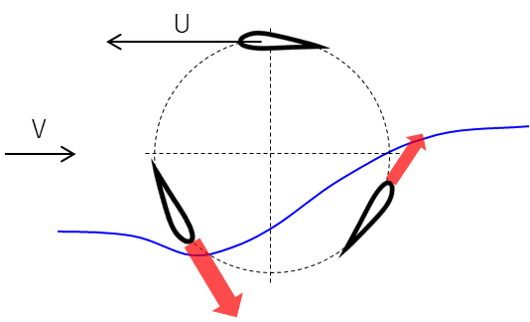
ダリウス風車(あるいはHダリウス風車)のブレード断面は翼型になっており、飛行機が揚力を得るのと同様に、流れを曲げながら推力(揚力)を得ます。そのため、ダリウス風車は揚力型風車に分類されます。
ダリウス風車のブレードうち、1つのブレードに着目し、それぞれの位置を(i)遡行区間 (ii)アビーム区間 (iii)順行区間 (iv)下流側アビーム区間と呼ぶことにします。(i)遡行区間では(U+V)の相対風を前方から受けます。(ii)アビーム区間では左からの風を上に曲げることで、その反力として下向きの力を受けて回転が強められます。(iii)順行区間では(U-V)の相対風を前方から受けます。(iv)下流アビームでは左からの風を下に曲げることで、その反力として上向きの力を受けて回転が強められます。ダリウス風車は風に押されて回転するわけではないので、λ= 1を超えて回転することができます。
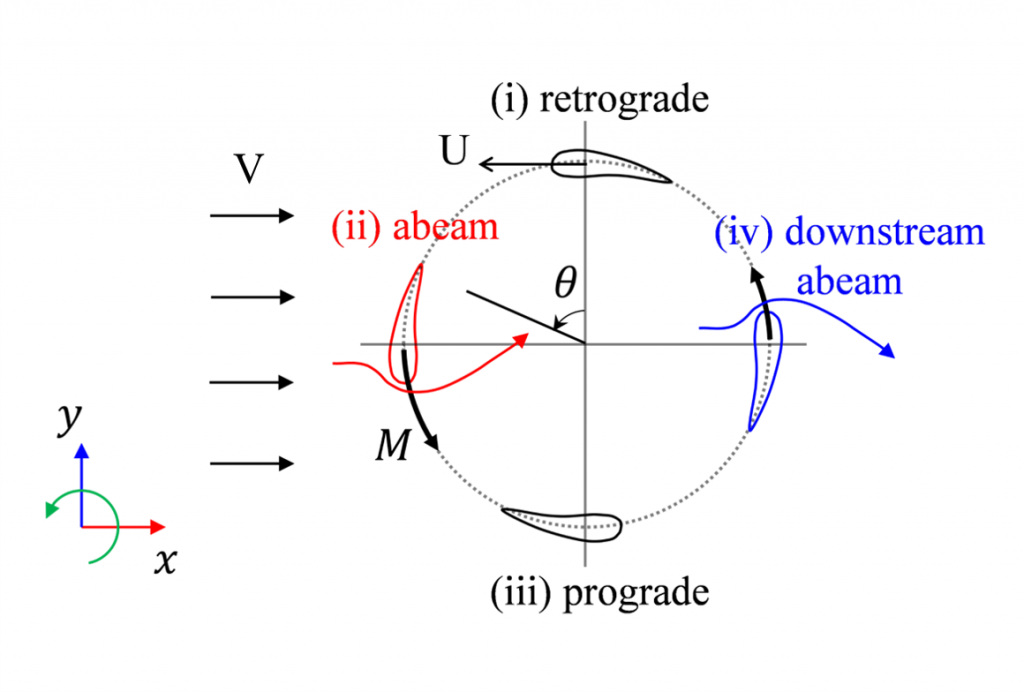
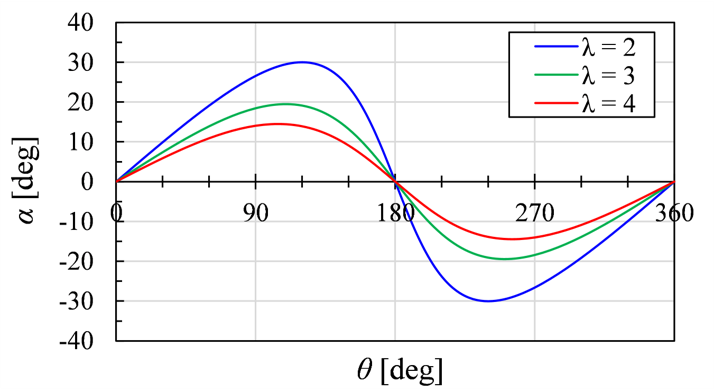
では、ダリウス風車の最適な周速比λはどの程度でしょうか。位置(回転角θ)と回転ブレードに対する相対的な風向(迎角α)の関係をみると、θ=120度とθ=240度において迎角αが最大になることが分かります。これらの角度はそれぞれアビーム区間と下流側アビーム区間に当たります。一般的な翼型ではα=15度程度で失速するので、λ< 3ではアビーム区間において失速してしまうことが予想されます。(失速とは、翼表面から流れが剥離してしまい抵抗が急増する現象です。)その場合、アビーム区間で得られるはずの大きい回転モーメントが得られません。従って、アビーム区間において失速しない程度の周速比が最適であると考えられます。また、周速比が大きすぎると迎角が小さくなり、十分に効率良く揚力が得られないため、そのような周速比は維持できません。
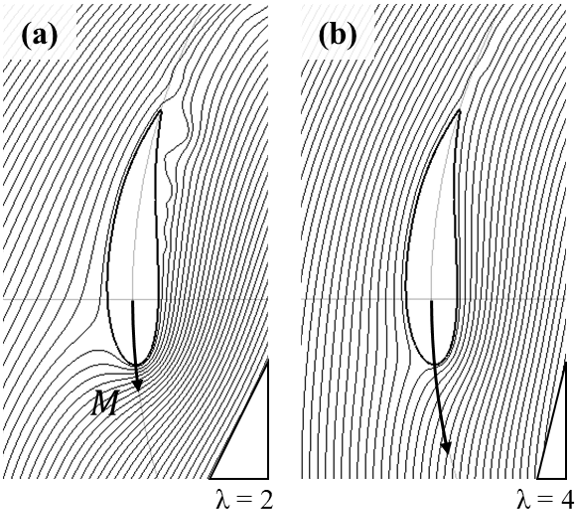
ブレードの失速についてより詳細に見てみましょう。アビーム区間においてブレードが失速してしまうと、左からの風を上に曲げる効果が弱まり、結果として風車の回転が弱まってしまいます。ブレードとともに回転する座標系におけるブレードまわりの流線に着目すると、(a)λ=2では翼後縁付近で流れが剥離している様子が見てとれます。一方、(b)λ=4では流れが翼表面に沿っており、失速の兆候は見られません。このことから、大まかな傾向として、一般的なダリウス風車は、λ>3では効率が良いが、λ<3では効率が悪いと言えます。失速しにくい厚翼を用いたり、ブレードを大きくしたり、ブレード数を増やしたりすることで、最適な周速比λを小さくすることができますが、これらの場合、回転抵抗が増えるため効率は低下しやすくなります。
垂直軸風車の効率
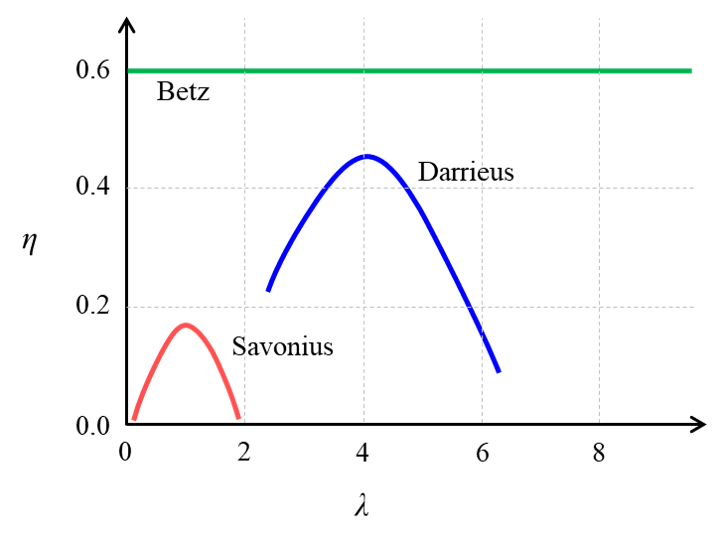
風車の発電量Pは回転モーメントMと角速度ωの積で表されます。風車の発電量P(=Mω)を、ある断面Sを通過する風の有するエネルギーの総量Q(=ρV3S/2)で正規化した値を発電効率η(=P/Q)と言います。つまり、効率は風のエネルギーのうち風車が回収する割合を表す指標です。上述の通り、サボニウス風車はλ≅1で効率が最大となり、ダリウス風車はλ≅4で効率が最大となります。また、サボニウス風車の効率は0.1~0.2程度、ダリウス風車の効率は0.4~0.5程度です。(実際の風車ではλとηの値は多少前後します。)ダリウス風車の方が高効率ですが、停止状態からの起動に難があります。一方、サボニウス風車は比較的低効率ですが、停止状態から自励回転に至ることが可能です。
停止状態からの起動(ダリウス風車)

ダリウス風車であっても、ブレード数を5枚程度まで増やせば、風のエネルギーだけで停止状態から自励回転に至ることが可能ですが、定格回転時の抵抗が増加してしまいます。
らせん状ブレードのHダリウス風車
Hダリウス風車のブレードをらせん状にすることで、ブレード数を増やさずに、定格回転時の抵抗増加を抑えつつ、自励回転による起動をしやすくします。
ダリウスとサボニウスのハイブリッド風車
ダリウス風車はλ<2では効率が低く、あるいは自励回転しないので、ダリウス風車を起動するためにサボニウス風車と組み合わせる場合があります。ただし、直径比が適切でないと、定格回転時にサボニウス風車が抵抗となってしまいます。例えば、ダリウス風車の直径をサボニウス風車の直径の3倍程度にすることで、自励回転により風車を起動させつつ、定格回転時にはダリウス風車とサボニウス風車がいずれも効率良く動作します。
風車による減風効果
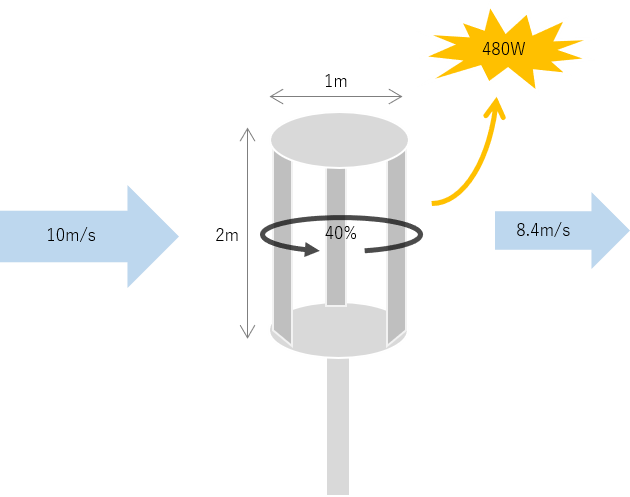
風速と風車の効率が分かれば、風車に回収されるエネルギー量が定まるので、風車を通過するエネルギー量も定まります。従って、下流側の風速が定まるので、減風効果を見積もることができます。
例えば、10m/sの風が効率40%(η= 0.4)の風車を通過すると、8.4m/sになります。また、効率40%の風車を3回通過すると10m/s → 8.4m/s → 7.1m/s → 5m/sとなり、風速が半減します。風車は風から効率良くエネルギーを回収するため、優れた減風装置だと考えられます。
サイクロローター
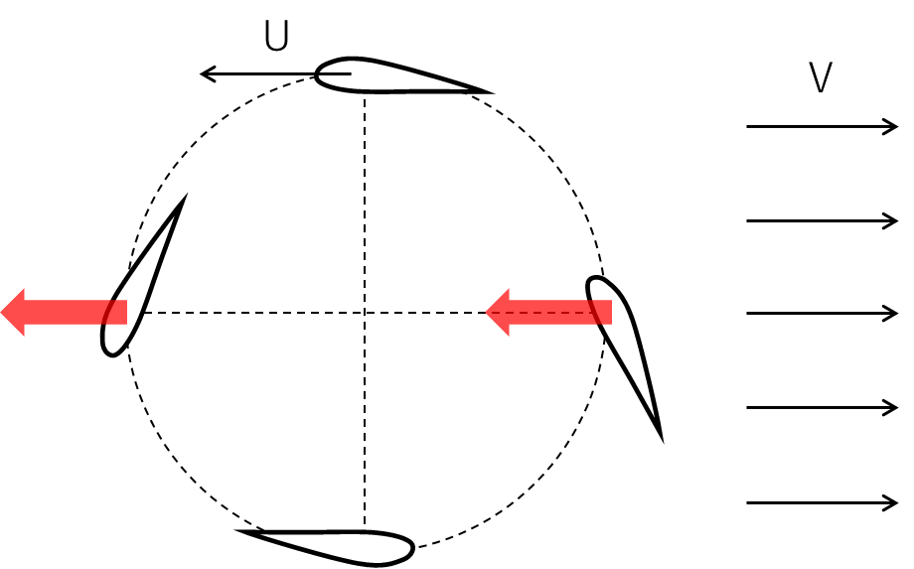
風力発電では、風のエネルギーを電気エネルギーに変換します。一方で、電気エネルギーを用いてプロペラを回し、風を発生させることで、プロペラ機やヘリコプター、ドローンの動力源とすることも可能です。同様に、ダリウス風車の原理を応用したサイクロローターも、ドローンの動力装置として研究が行われています。サイクロローターでは、ブレードのピッチ角を制御することで任意の方向にアビーム状態(および下流側アビーム)を作り出し、機体を傾けることなく360度あらゆる方向に風を発生させることができます。(https://en.wikipedia.org/wiki/Cyclorotor)