Nagareは、計算流体力学研究所(iCFD)が提供する流体解析サービスの総称です。
Nagareでは、Navier–Stokes方程式の数値解を求めるにあたり、離散化が基礎方程式に与える影響を極力抑え、方程式が本来持つ力学的な性質を損なわずに解くことを基本方針としています。
この方針は、特定の条件における結果の再現(実験結果との一致など)を最優先とするものではありません。むしろ、解法の普遍性を高めることで、流れの構造が十分に把握されていない未知の現象に対しても適用可能な手法を提供することを目指しています。また、物理モデルや経験則によってあらかじめ想定された流れ像へ解析結果を収束させるのではなく、Navier–Stokes方程式から自発的に生じる流れを、可能な限り素直に捉えることを重視しています。
その結果、想定されていなかった流れの構造が顕在化し、現象に対する理解や問題設定そのものを見直す契機となる場合があります。Nagareは、実験や観測、既存の実務的な解析手法を代替するものではなく、それらと補完的に活用されることを想定しています。
以下では、こうした基本方針を支える離散化手法について概説します。
陽解法による非定常解析(時間離散化)
Nagareでは、Navier–Stokes方程式の移流項を線形化することなく、陽解法により非線形性を保ったまま時間発展させます。これにより、流れの時間的な応答、特に非定常性の強い流れにおける構造の生成・発達・消滅といった過程を、時間発展として直接捉えることが可能になります。
移流項の線形化や定常化を前提とした解法は、計算効率や安定性の面で利点を持つ一方で、非定常現象に固有の時間スケールで生じる相互作用が、暗黙のうちに平均化・抑制されてしまう傾向があります。
スタガード格子(空間離散化①)
Nagareでは、スタガード格子[1]を採用しています。スタガード格子は、速度成分と圧力を空間的にずらして配置することで、離散化された格子系においても質量保存と運動量保存が自然に満たされる特徴を持ちます。
この配置により、圧力場における数値的な奇偶振動を抑制すると同時に、連続の式と運動量方程式が格子レベルで局所的に結合されます。スタガード格子は、Navier–Stokes方程式が本来持つ保存特性を離散空間上に写像するための基盤となるものです。
DNS & ILES(空間離散化②)
移流項の空間離散化には、自乗量保存特性を有する4次精度中心差分[2](境界付近では2次精度)を用いています。この離散化は、粘性や外力を伴わない理想系において、離散化に起因する運動エネルギーの数値的な生成や散逸が生じないという性質を持ちます。
これは単なる高精度化を目的としたものではなく、Navier–Stokes方程式が内包する保存特性を、離散系においても可能な限り再現することを意図した選択です。Nagareでは、安定性の確保に先立ち、まず基本的な離散化が力学的に中立であることを重視しています。
一方で、急峻な速度勾配などの局所的な非線形作用が卓越する場合には、中心差分のみでは分散誤差に起因する数値振動が顕在化することがあります。その際には、UTOPIAスキーム[3]に基づく数値粘性を補助的に導入します。この数値粘性は常時支配的に作用するものではなく、数値解が物理的に許容される範囲を逸脱しようとする領域において、局所的かつ必要最小限に機能します。
この構成により、保存性に優れた離散化の性質を維持したまま計算の安定性を確保することが可能となります。その結果、計算格子で解像可能なスケールにおいてはDNSに近い振る舞いを示し、未解像スケールに対しては離散化と数値粘性の性質に基づいて暗黙的にエネルギー移送が表現されるという点で、Nagareの手法は、Implicit LES (ILES)として解釈可能な性質を持ちます。
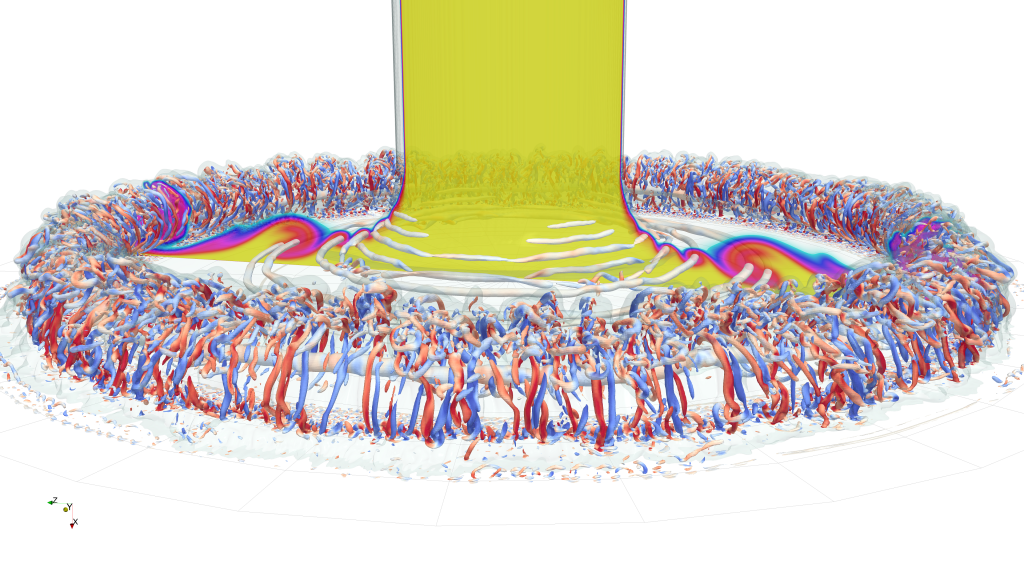
Nagareによる解析事例①:ダウンバースト状の衝突噴流
本解析は、ダウンバーストが地表に衝突することで誘発されたKelvin–Helmholtz不安定によりガストフロントが形成され、その内部に発達する縦渦構造を捉えた事例です。ガストフロント内部に存在する強い乱流場を、乱流モデルによって平均化することなく直接解くことで、無秩序な乱流ではなく、縦渦群から成る秩序的な流れの構造であることを明らかにしました。
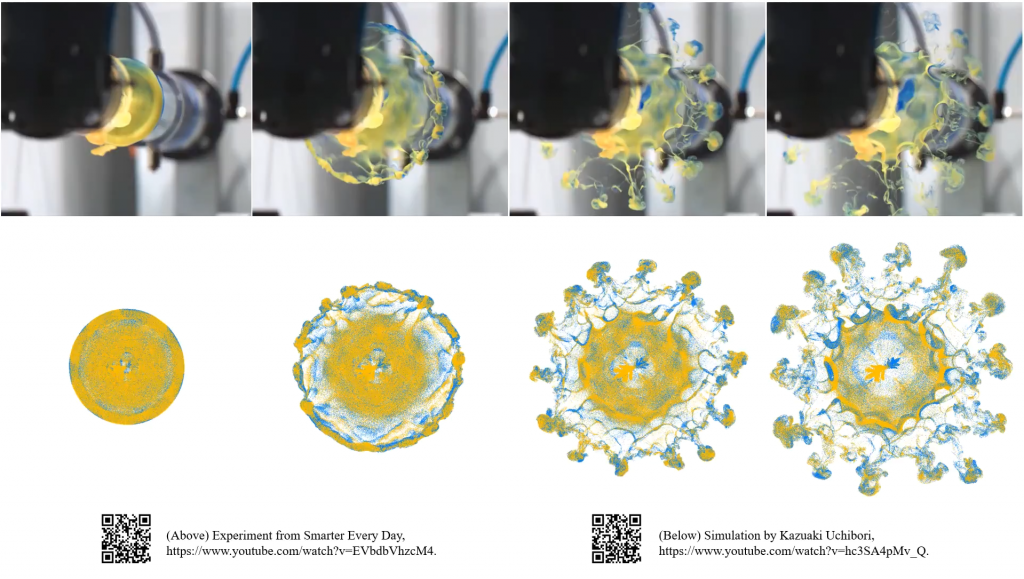
Nagareによる解析事例②:渦輪の正面衝突
参考文献
[1] 梶島岳夫,『乱流の数値シミュレーション』,養賢堂,1999,ISBN 978-4-8425-0603-6.
[2] Y. Morinishi, T. S. Lund, O. V. Vasilyev, and P. Moin, “Fully conservative higher order finite difference schemes for incompressible flow,” J. Comput. Phys., Vol. 143, No. 1, pp. 90–124, 1998.
[3] B. P. Leonard, M. K. MacVean, and A. P. Lock, “Positivity-preserving numerical schemes for multidimensional advection,” NASA Technical Memorandum 106055 (ICOMP-93-05), NASA, March 1993.